As of August 29, 2001, SETI@home users have detected billions of spikes and hundreds of millions of gaussians, pulses, and triplets. (For a current tally of detected signals, visit our page on finding candidate signals).

Clearly, identifying these signals is only one step in the search for extraterrestrial communication. First of all, these results need to be verified, as discussed in Newsletter #8. Second, signals due to radio frequency interference (RFI) need to be removed from consideration. Also, we try to identify signals that are "persistent"—consistent in location and frequency across time. The goal of this newsletter is to explain SETI@home's current procedure in identifying persistent signals and provide specific examples to illustrate this process.

Why is Persistency Important?

We expect most (if not all) of our detected radio signals to originate from transmitters on Earth, satellites, galactic noise, and other natural astronomical phenomena. If our radio telescope happens to point toward Alpha Centauri while detecting radio signals from a television broadcast that passes overhead, all we know from our data is that we detected a signal while looking at Alpha Centauri. However, if we continue to detect a signal on multiple occasions while pointing toward Alpha Centauri, it becomes less likely that a signal from Earth is the culprit and more likely that we're truly getting a signal from that region in space. Thus, a key task is to identify signals that detected at multiple times from the same location in the sky.

Signal Matchmaking

To find persistencies, we match signals together that were detected at different times within 2.5 arcminutes of the same right ascension (RA) and declination (DEC) coordinates in the sky, and that share the same frequency band (within 50Hz). (For an explanation of RA and DEC, read our page on features of skymaps.)

The more matches we find for a particular location in space, the more confident we are about a persistent signal coming from that area of the sky. The bar graph below provides a snapshot (from August 29, 2001) of an ongoing persistency matching process for gaussian signals. It reports the number of persistent gaussians found, with separate bars for 1, 2, 3, and 4 (or more) matches at specific locations in the sky. More matches means better persistency. A similar graph on our current progress summary page is updated regularly.

# of Persistency Matches out of 80,704 Gaussians 2,868 1   111 2   4 3   0 4+

An Example

Let's take a closer look at a gaussian with persistent matches. Clicking the image to the left will take you to a set of four persistency graphs. (To learn more about these graphs please see "Key Features of Persistency Graphs".) The main purpose of these graphs is to check the context around a persistent signal to find clues to the source of the signal. Some graphs are clickable, allowing you to view plots broken down by time, power, or score, as well as view plots showing nearby gaussians, spikes, pulses, or triplets. As you can see, there's quite a bit to explore for just one persistent signal.

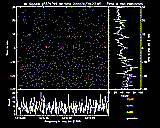
Some graphs in this set break down signal distributions for gaussians, spikes, triplets, and pulses occurring closely in time and frequency to matched persistent signals. For example, this graph shows a pattern of signals occuring in the same vertical band as the target signal. Such a pattern suggests a source of rfi that is continuously detected (at a specific frequency and power) even as the telescope moves across the sky.

By finding persistent signals and removing RFI-related signals from consideration, we can significantly narrow the number of viable candidates requiring further detailed examination. We will continue to keep you updated as our process continues.

Return to Science Newsletter main menu