Consistency of non-barycentric multiplets
Message boards :
Nebula :
Consistency of non-barycentric multiplets
Message board moderation
| Author | Message |
|---|---|
 David Anderson David Anderson Send message Joined: 13 Feb 99 Posts: 176 Credit: 502,653 RAC: 0 |
Eric and I have mostly been working on multiplet scoring: estimating the likelihood that a set of signals is something other than noise. This is work in progress and I'll report on it later. I had some new ideas about finding non-barycentric multiplets. Recall that these are things we'd expect to hear from transmitter that sends a constant frequency and is in an accelerated reference frame: e.g. on the surface of a planet that's orbiting a star, or in orbit around such a planet, or in orbit around a star. The signal from such a transmitter would reach us with a time-varying Doppler-shift, reflecting the change in the transmitter's radial velocity in our direction. The amount of this shift, and its rate of change, would depend on various physical parameters: the size and period of the orbit, the rotational period, and so on. Eric has established plausible ranges for these parameters, based on what's known about actual stars and extrasolar planets. Given these ranges, the frequency range of a non-barycentric signal could be as much as 200 KHz. In terms of finding non-barycentric multiplets, the general situation is that we're processing a particular pixel (sky location). This pixel was observed some number of times, on the order of 10. Each observation is on the order of 10 seconds. We're considering a particular 200 KHz frequency band. Within each observation there may be signals sprinkled across the entire band. This is shown here: 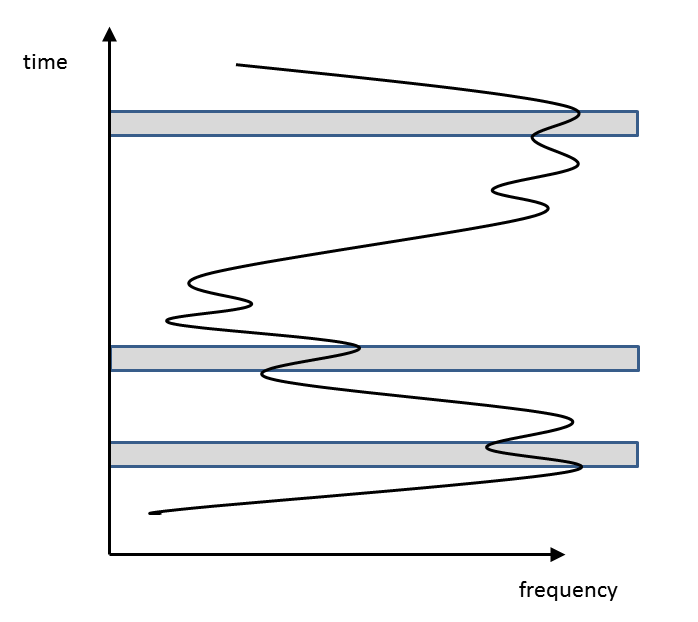 Gray bands are observation periods. The wiggly line is the kind of transmission we're looking for; the fast wiggles are rotation, the slow wiggles are orbit. Out of all these signals, we're trying to find a subset (a "multiplet") that
|
|
Sesson Send message Joined: 29 Feb 16 Posts: 44 Credit: 1,353,463 RAC: 3 |
I remembered Einstein@home search for pulsars. They try to fit the data with a set of potential orbital parameters. This is very similar to SETI@home's search, except that SETI@home data is not continuous, more like Asteroid@home. It might lead to increased sensitivity as well as ability to making a statement about "no SETI signal with power greater than X", something like Einstein@home publications about continuous GW. |

©2025 University of California
SETI@home and Astropulse are funded by grants from the National Science Foundation, NASA, and donations from SETI@home volunteers. AstroPulse is funded in part by the NSF through grant AST-0307956.