Interesting Physics
Message boards :
Science (non-SETI) :
Interesting Physics
Message board moderation
Previous · 1 · 2 · 3 · 4 · 5 · 6 · 7 . . . 19 · Next
| Author | Message |
|---|---|
 tullio tullio Send message Joined: 9 Apr 04 Posts: 8797 Credit: 2,930,782 RAC: 1 
|
So far a quantum computers des not exist, although D-Wave has sold a couple of them, but there is a strong doubt about them being real quantum computesr. AFAIK Anton Zeilinger has succeded in teleporting photons up to 143 km (see the Zeilinger Bibliography). A team of Italian scientists has teleported photons to an orbiting satellite, via optics. Maybe this last priority regards only photons teleported via fiber. Tullio |
 janneseti janneseti Send message Joined: 14 Oct 09 Posts: 14106 Credit: 655,366 RAC: 0 
|
So far a quantum computers des not exist, although D-Wave has sold a couple of them, but there is a strong doubt about them being real quantum computesr. Tullio AFAIK the D-Wave computers only use the method not the technology of QM. |
 tullio tullio Send message Joined: 9 Apr 04 Posts: 8797 Credit: 2,930,782 RAC: 1 
|
They use a cryogenic chip developed by them and a kind of ground state search also developed by them. It is is more an analogic coprocessor than a quantum computer. Tullio |
|
KLiK Send message Joined: 31 Mar 14 Posts: 1304 Credit: 22,994,597 RAC: 60 
|
"Scotty, they beamed some photons 100km away!" "How primitive...we can show them how it's done." :D LoL   non-profit org. Play4Life in Zagreb, Croatia, EU |
 William Rothamel William Rothamel Send message Joined: 25 Oct 06 Posts: 3756 Credit: 1,999,735 RAC: 4 
|
We all know what Q-bits are--I think--. Explain how they are ideal for factoring and how this could be done more expeditiously than a super-computer using two-state logic. Can you write a program to add 2 and 2 in qubit logic. How do you represent a 2 ? |
 janneseti janneseti Send message Joined: 14 Oct 09 Posts: 14106 Credit: 655,366 RAC: 0 
|
We all know what Q-bits are--I think--. Explain how they are ideal for factoring and how this could be done more expeditiously than a super-computer using two-state logic. Can you write a program to add 2 and 2 in qubit logic. You need to be able to use Dirac—or "bra–ket" notation to do that. But here are some links. https://en.wikipedia.org/wiki/Shor%27s_algorithm Here is a lot how it works. Basic concepts in quantum computation. http://www.quantiki.org/wiki/Basic_concepts_in_quantum_computation Qubit Physical representation https://en.wikipedia.org/wiki/Qubit#Physical_representation The arithmatic reminds of complex number. |
 tullio tullio Send message Joined: 9 Apr 04 Posts: 8797 Credit: 2,930,782 RAC: 1 
|
A qubit can represent two states. 2 qbits repersent 4 states, 3 qubits 8 states, 4 qubits 16 states, 5 qubits 32 states and so on. Th problem is when you want to read the answer of a calculation. You must collapse a kind of wavefunction to a number.So far real quantum computers have factored 8 qubits and no more. Tullio |
 janneseti janneseti Send message Joined: 14 Oct 09 Posts: 14106 Credit: 655,366 RAC: 0 
|
A qubit can represent two states. 2 qbits repersent 4 states, 3 qubits 8 states, 4 qubits 16 states, 5 qubits 32 states and so on. Th problem is when you want to read the answer of a calculation. You must collapse a kind of wavefunction to a number.So far real quantum computers have factored 8 qubits and no more. The wave function is called superposition that means you can have both states at the same time. Quantum superposition is a fundamental principle of quantum mechanics. It states that much like waves in classical physics, any two (or more) quantum states can be added together ("superposed") and the result will be another valid quantum state; and conversely, that every quantum state can be represented as a sum of two or more other distinct states. Mathematically, it refers to a property of solutions to the Schrödinger equation; since the Schrödinger equation is linear, any linear combination of solutions will also be a solution. |
 William Rothamel William Rothamel Send message Joined: 25 Oct 06 Posts: 3756 Credit: 1,999,735 RAC: 4 
|
Transistor logic (Binary) has two states. Qubits have three states do they not. If I want to add 2 and 2 on a digital computer I represent the numbers two by .....010 in registers. I then examine: .....010 .....010 with an adder (Boolean Exclusive OR plus Boolean AND) and a carry function and I would get .....100 with a 0 carry to the fourth position The logic circuit for the last three bits of the adding register would look as shown below with carry in and carry out. 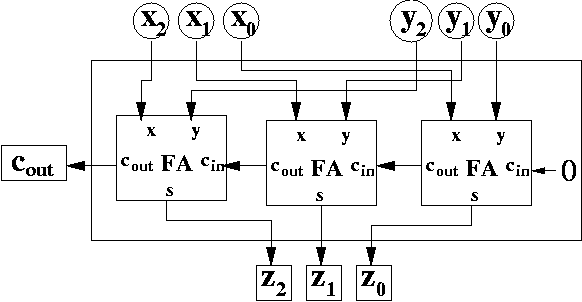 The three blocks are Full Adders whose logic circuit configurations are well known so like I said help me understand by showing how you would do this on a quantum computer. |
 janneseti janneseti Send message Joined: 14 Oct 09 Posts: 14106 Credit: 655,366 RAC: 0 
|
Addition 2+2=4 with qubit bar-ket notation. |2> |2> ------ |4> Quantum register of size three can store individual numbers such as 3 or 7, but, it can also store the two of them simultaneously. => 1 / square(2) * (|3> + |7>) In fact we can prepare this register in a superposition of all eight numbers -- it is enough to put each qubit into the superposition. |0> + |1> + |2> + |3> + |4> + |5> + |6> + |7> ignoring the normalisation constant 1 / square(2) |
 William Rothamel William Rothamel Send message Joined: 25 Oct 06 Posts: 3756 Credit: 1,999,735 RAC: 4 
|
Still not seeing the logic involved nor the physical circuit. To start with: What are the states of a Qubit ? is it yes, no, maybe or 0, 1, and ? do we use base three here ? Do we have Quantum: Logic, Venn Diagrams, Karnaugh maps?? |
 janneseti janneseti Send message Joined: 14 Oct 09 Posts: 14106 Credit: 655,366 RAC: 0 
|
Still not seeing the logic involved nor the physical circuit. To start with: What are the states of a Qubit ? is it yes, no, maybe or 0, 1, and ? do we use base three here ? Qbits and bits can only have two states. But a qubit can also have a superposition so one qubit can have two states at the same time. Tullio explained that. And you can use any base you want. I prefer decimal. Or hexadecimal. |
 tullio tullio Send message Joined: 9 Apr 04 Posts: 8797 Credit: 2,930,782 RAC: 1 
|
Quantum computers are nt built to do things that digital computers do well. A typical problem is that of factoring a huge number. Take two large primes, multiply them and you get a huge number which is not prime. To factorize it you can try the Eratothenes sieve method, used for searching prime numbers. You divide it by 2, then by three, then by 5 and so on. This takes a vry long time. A quantum computer should need only a single division. Tullio |
 janneseti janneseti Send message Joined: 14 Oct 09 Posts: 14106 Credit: 655,366 RAC: 0 
|
Until now in factoring numbers using quantum computers only have found 15, 21, 143 and 56153. http://phys.org/news/2014-11-largest-factored-quantum-device.html "We're still a far way from outperforming classical computers," Dattani told Phys.org. "The highest RSA number factored on a classical computer was RSA-768, which has 768 bits, and took two years to compute (from 2007 to 2009)." RSA numbers are a set of large "semiprimes"—numbers with exactly two prime factors. RSA numbers are particularly special due to the difficulty in factoring them. For this reason, they are used by governments, militaries, and banks to keep financial information secure. |
 tullio tullio Send message Joined: 9 Apr 04 Posts: 8797 Credit: 2,930,782 RAC: 1 
|
I've read on "Nature" that cryptographers in banks and military institutions are worried about quantum computers ability in factorizing numbers, since security of RSA and other cryptographyc methods are based upon the assumption that very large numbers are difficult to factorize. If this is no longer true, they should adopt other methods, which are being studied. On the other hand, quantum criptography has already been used in Swiss cantonal elections to safely distribute cryptographic keys. Tullio |
 janneseti janneseti Send message Joined: 14 Oct 09 Posts: 14106 Credit: 655,366 RAC: 0 
|
But is it not the reason to use quantum computers only about distribute cryptographic keys. From what I have heard that Eve cannot evesdrop on quantum keys/messages without Alice and Bob knows that. |
 tullio tullio Send message Joined: 9 Apr 04 Posts: 8797 Credit: 2,930,782 RAC: 1 
|
This is the only practical application so far. The rest lies in the future. Tullio |
 William Rothamel William Rothamel Send message Joined: 25 Oct 06 Posts: 3756 Credit: 1,999,735 RAC: 4 
|
Still would like to know why so called quantum computers are good at factoring and exactly why and how the "circuitry" and logic works. |
 janneseti janneseti Send message Joined: 14 Oct 09 Posts: 14106 Credit: 655,366 RAC: 0 
|
Still would like to know why so called quantum computers are good at factoring and exactly why and how the "circuitry" and logic works. Hmm. Quantum computers are only good at factorizing. Classical computers are not. And exactly why and how the "circuitry" and logic works. Their is no such thing as Exact events in the quantum world. Only Probabilities. Here is what you have to know if you want to know how a quantum computer works. http://www.quantiki.org/wiki/Basic_concepts_in_quantum_computation |
 William Rothamel William Rothamel Send message Joined: 25 Oct 06 Posts: 3756 Credit: 1,999,735 RAC: 4 
|
Their is no such thing as Exact events in the quantum world. Well then if true then we could never have a useful result nor a piece of actual hardware. It's time for all of us pseudo intellectuals to come out from hiding behind the term "quantum" and get to discussing real logic, problems, circuitry or small atomic structures and results in the Quantum world. There are in fact true and actual events in the quantum world or else we would not have spectroscopy. Perhaps the term "quantum" has been applied to too many things that we don't fully understand or have a good explanation for. |

©2024 University of California
SETI@home and Astropulse are funded by grants from the National Science Foundation, NASA, and donations from SETI@home volunteers. AstroPulse is funded in part by the NSF through grant AST-0307956.