ASTR 10, Vista College, Spring 2004 - Instructor: Korpela

HW #4 -- Due Apr 15, 2004

Explain ALL answers.

Determining Properties of Stars

1. Parallax (15 points)

   1. Imagine that you are looking at the stars from Earth in January. Do the following on the Figure (not to scale!) below (turn the page):
      • Use a straightedge or a ruler to determine which of the distant stars Star A appears closest to in your night sky. Circle this star and label in "Jan".
        
      • Repeat for July and label the point "July".
      • Draw a dotted line from the Sun thorugh star A to the distant stars.
      • The parallax angle is the small angle, just below Star A, formed by the dotted line and one of the lines you drew above. Label this angle P_A.
      
   2. In the figure below, these same distant stars are shown as you would see them in the night sky.
      
      • In this box, draw a small "x" to indicate the position of star A as seen in January, and label in "Jan".
      • In the same box, draw another "x" to indicate the position of Star A as seen in July and label it "July".
   3. Describe the motion of Star A relative to the distant stars from January of one year, through July, to January of the following year.
   4. Consider the following discussion between two students regarding the relationship between parallax angle and the distance we measure to a star:
      Student 1: If the distance to the second star is larger, then the parallax angle will be larger. Larger distance means larger angle.
      Student 2: If we drew a diagram for a star that was much farther away from us, then the triangle in the diagram would be pointier than the one we just drew. That should make the parallax angle smaller for a star farther away.
      Do you agree with Student 1, Student 2, both, or neither? Why? (Hint: If you're confused, place a second star (labelled "B") on the first diagram (farther from the Earth), and repeat the steps above.)
   5. Extra Credit: Why are parallax measurements limited to the nearest stars? (Hint: What causes the change in apparent position?)

2. Masses of Stars (15 points)

   1. Why does the orbital period of a binary star depend on its mass? Explain in terms of gravity.
   2. Why can't we know the velocity of the stars in a spectroscopic binary without knowing the inclination (tilt of the orbit relative to us) of the system?
   3. How do we know the inclination (and therefore stellar velocities) of an eclipsing binary system?

3. Velocities (5 points)

   True or False (explain your reasoning): We can determine the space velocity of a star simply by looking at how it moves across the sky over time.

   H-R Diagram (20 points)

   Use the H-R diagram below to answer the following questions:
   
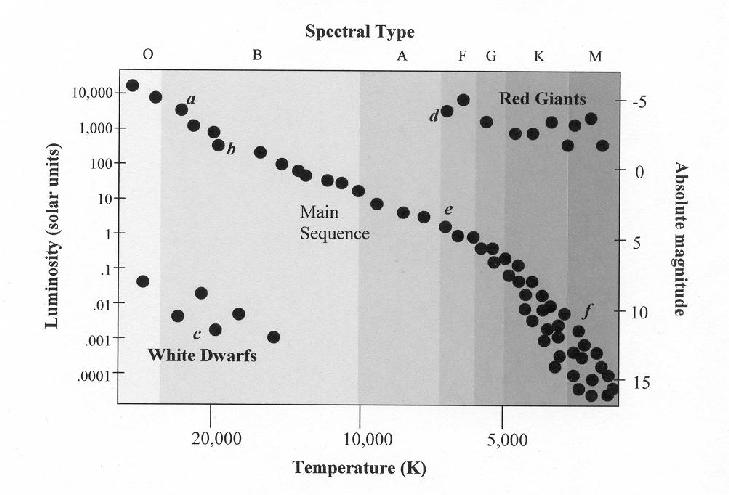
4. (8 points) For each question below, state whether the star would be a red giant, a white dwarf, or a main sequence star, and provide the letter of a star from the HR diagram that fits the description.
   1. very bright (high luminosity) and cool (low temperature)
   2. very dim and very hot

5. (12 points) By measuring their temperatures and analyzing their spectra, we have determined that stars "a" and "f" are both main sequence stars as shown on the diagram. Suppose they have the same apparent brightness.
   1. Which one is more luminous (intrinsically brighter)?
   2. Which one is farther away (explain!)?
   3. With only the measurements mentioned, can we determine their actual distances?
   4. Extra Credit: If we didn't need parallax to determine the distances to these two stars, why do we need to use parallax at all?

6. Stellar Population, Apparent vs Intrinsic Brightness (10 points)

   1. What kind of star is the most common? (ie red giant, blue main sequence star, etc.)
   2. If you look only at the (apparently) brightest stars in the night sky, what kind of star are you likely to be observing? Why?
   • Hint: The most common stars are not necessarily the most commonly seen!

   Stellar Structure and Energy Generation - Comparing Theory and Observation

7. Testing the Solar Model (20 points):
   • What are the ingredients that go into making a model of the Sun? (Hint: What laws of physics/quantities are assumed and used in the model?)
   • Explain how observations of netrinos from the Sun can be used to test our model of the Sun.
   • What are the results of these experiments, and why do they present a challenge for solar models?
   • How might we resolve the discrepancy between the theoretical prediction and the observations without changing our theory of stellar structure?
   • Extra Credit: What other measurement technique (ie not neutrinos) has been used to investigate the structure of the Sun?

8. Mass-Luminosity Relation (5 points): How does the theory of stellar structure explain the observed mass-luminosity relation?

9. (10 points): Why is there a lower limit to the mass of a main-sequence star?