Trying to understand RA and DEC coordinates
Message boards :
SETI@home Science :
Trying to understand RA and DEC coordinates
Message board moderation
| Author | Message |
|---|---|
 S@NL - d.3ssen S@NL - d.3ssen Send message Joined: 12 Mar 07 Posts: 9 Credit: 244,893 RAC: 0 
|
I'm trying to figure out how to read and convert the RA/DEC coordinates in the NTPCkr threads to Google Sky. After reading up on Right Ascension, Declination and the Celestial Equatorial Coordinate System on several sites, I still can't get my head wrapped around the conversion I need to make to find the candidates from the NTPCkr on Google Sky. As I understand from various sites the RA is usually displayed has Hours:Minutes:Seconds, however, NTPCkr threads only shows a degree unit. (like RA: 22.895508). As some sites explain the full 360 degree of our globe is divided into 24 hours. As such, 15 degrees = 1 hour. So, 22 degrees would be a little over 1 hour. So in Google Sky I would point my cursor to 1h. But then comes the tricky part...what about the .895508? If 1 degree = 1h / 15 degrees = 0.066666h. And 0.066666h * 60m = 4 minutes. So .895508 degrees would be 4 minutes. According to this calculation, in Google Sky I would have to point my cursor to 1h 4m 00.0s Am I correct? |
 Bob DeWoody Bob DeWoody Send message Joined: 9 May 10 Posts: 3387 Credit: 4,182,900 RAC: 10 
|
You multiply the 0.895508 by 60 (the number of minutes in a degree) getting 53.73048 minutes then multiply the .73048 times 60 again to get 43.82 seconds arriving at 22 degrees 53 minutes 43.82 seconds. ( I think ) Try using celestia or Stellarium to get a better grip on celestial coordinates Bob DeWoody My motto: Never do today what you can put off until tomorrow as it may not be required. This no longer applies in light of current events. |
 William Rothamel William Rothamel Send message Joined: 25 Oct 06 Posts: 3756 Credit: 1,999,735 RAC: 4 
|
it is a simple idea of shooting a line of sight into the heavens. This is just a triangle with a given angle. (Declination) it is probably measured from the plane of rotation of the Earth (Not the ecliptic but most probably the plane of rotation of the Earth at the equinox)). The you just need to figure out where to rotate the base of the triangle to hit your desired spot in the cosmos. This is the right ascension (eastward along the equater from a fixed reference point. 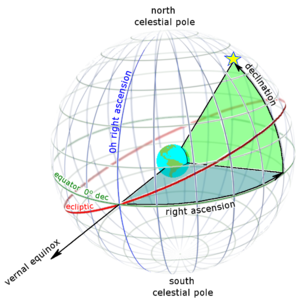 |
|
bluestar Send message Joined: 5 Sep 12 Posts: 7031 Credit: 2,084,789 RAC: 3 |
I notice that a couple of threads have became locked. There are a couple of good ideas behind all of this when reading through. Although I am not being an active astronomer when it comes to visually observing the sky, here is one point to notice. You certainly know that the Earth is having a rotation period along its axis in about 24 hours (23 hours 56 minutes), also wobbling on its axis by means of nutation and the slower precession. https://en.wikipedia.org/wiki/Nutation https://en.wikipedia.org/wiki/Precession Also looking up "Aberration" and "Twinkling" as well, but these two subjects are not what I want. The third word or description for this I therefore do not have right now. Because when you are standing on top of a mountain and an earthquake is happening, you are supposed to be falling down, but not when you are standing at the foot of the same mountain. Therefore have a look at the equinoxes along the celestial equator in order to observe this. The angle in which the ecliptic crosses the equator from south to north in the autumn sky and from north to south in the spring sky is the same as the angle of the poles of the earth when aligned towards the sun, namely 23 degrees, 27 arc minutes. Because of the precession, the absolute celestial coordinates is being seen or observed moving in a south-west direction in the autumn sky, making alpha Capricori higher up in the sky and more accessible each year after the end of summer. Similarly, alpha Librae should be moving the same way as well in the spring sky when the winter is nearing end. Therefore it should be possible to assume that the direct angle of the light from the sun reaching the equator of the Earth, like in Africa, should then be able to continue through the central core of the earth and then vanish in space when reaching equator on the other side. Such a thing is of course not happening. This depends where on the equator the light of the earth is hitting, of course. In the end such things become slightly hypothetical, but at least a correct answer to this question should be possible to give. I think this should be explaining this without going into too much detail. |
 S@NL - d.3ssen S@NL - d.3ssen Send message Joined: 12 Mar 07 Posts: 9 Credit: 244,893 RAC: 0 
|
You multiply the 0.895508 by 60 (the number of minutes in a degree) getting 53.73048 minutes then multiply the .73048 times 60 again to get 43.82 seconds arriving at 22 degrees 53 minutes 43.82 seconds. ( I think ) This made the most sense to me. So I'm going to try and use these calculations to get a more precise location on Sky. Also thinking about trying the programs you mentioned. |

©2024 University of California
SETI@home and Astropulse are funded by grants from the National Science Foundation, NASA, and donations from SETI@home volunteers. AstroPulse is funded in part by the NSF through grant AST-0307956.